|
With the discovery in the early 20th century
that spiral-shaped nebula were, in fact, other galaxies external to our
own, our concept of a Universe became one of in a Newtonian universe of
infinite size and mass, galaxies spread out in infinite space. However,
there is a problem with a uniform, static Universe, any density
enhancements would become unstable to gravitational
collapse. Thus, the whole Universe should have collapsed (or be
collapsing) into a giant black hole.
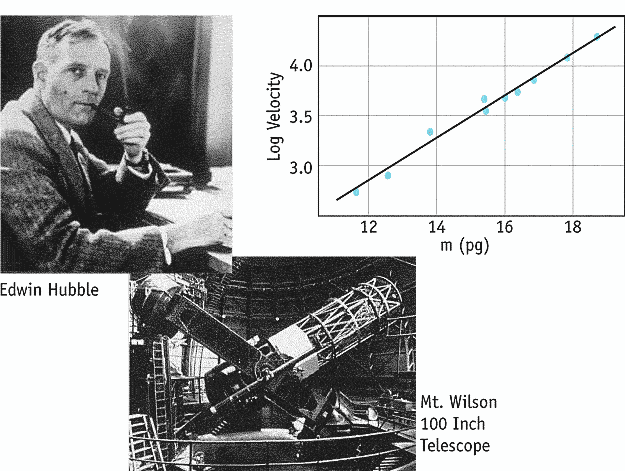
.. In the 1930's, Edwin Hubble discovered that all galaxies have a positive redshift. In other words, all galaxies were receding from the Milky Way. By the Copernican principle (we are not at a special place in the Universe), we deduce that all galaxies are receding from each other, or we live in a dynamic, expanding Universe. This solves the problem for gravitational collapse, only small regions will collapse to form galaxies. The rest of space keeps expanding. |

.. |
.. The expansion of the Universe is described by a very simple equation called Hubble's law; the velocity of the recession of a galaxy (determined from its redshift, see below) is equal to a constant times its distance (v=Hd). Where the constant is called Hubble's constant and relates distance to velocity in units of megaparsecs (millions of parsecs). .. The velocity of a galaxy is measured by the Doppler effect, the fact that light emitted from a source is shifted in wavelength by the motion of the source. The change in wavelength, with respect to the source at rest, is called the redshift (if moving away, blueshift if moving towards the observer) and is denoted by the letter z. Redshift, z, is proportional to the velocity of the galaxy divided by the speed of light. Since all galaxies display a redshift, i.e. moving away from us, this is referred to as recession velocity. |
.. |
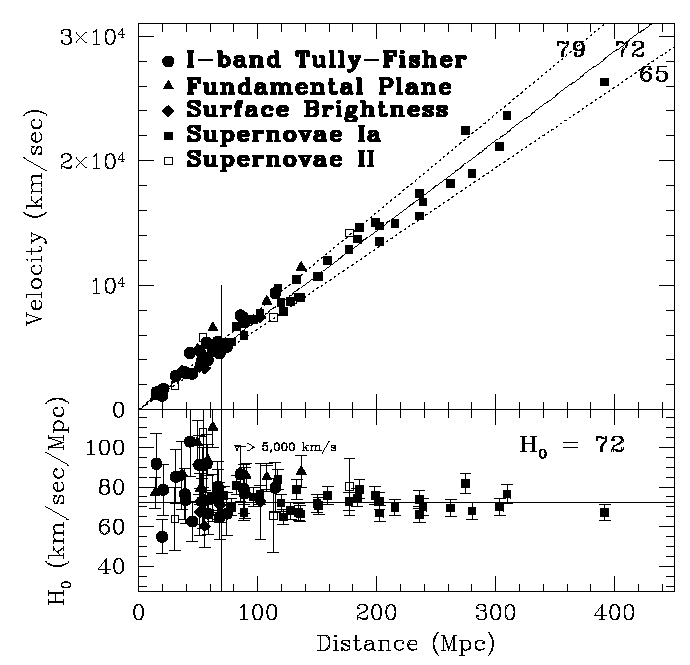
.. As a result, distance scale work uses a chain of distance indicators working outward from nearby stars to star clusters in our own Galaxy to stars in nearby galaxies. Unusually bright stars, such as variable stars and supernovae, complete the distance ladder out to cosmological distances. The latest results from the Hubble Space Telescope are shown above, a plot of recession velocity with distance (in megaparsecs, millions of light-years). The straight, linear correlation indicates that the Universe is currently expanding at a rate of 72 km per sec for every Mpc. The rate, known as Hubble's constant, may change with time (see next lecture). |
|
A common question in cosmology is "why are
all the galaxies receding from each other?" In other words, the
cosmological principle requires that we not be at a special place in the
Universe. Since all the galaxies are moving away from us, then they must
all be moving away from each other. This is explained if the Universe, as
a whole, is expanding.
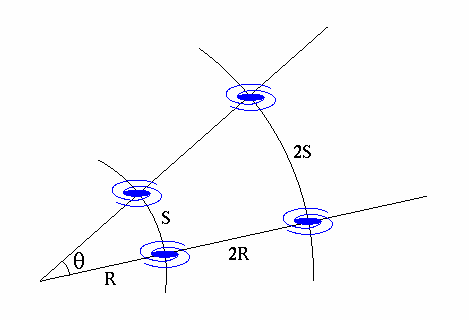
.. In a real sense, Hubble's law, the recession velocity of galaxies, is an illusion. The galaxies are not moving, the space between them is literally expanded. To see how this produces a Doppler effect, consider a simply Universe that is a circle. To the observers in this type of Universe, they believe they live in a 1D structure. But, in fact, they live in a 2D structure, a circle. The position of the galaxies can be measured by the distance between them (S, see diagram below) or what are called the co-moving coordinates, an angle q between the galaxies. |
.. |
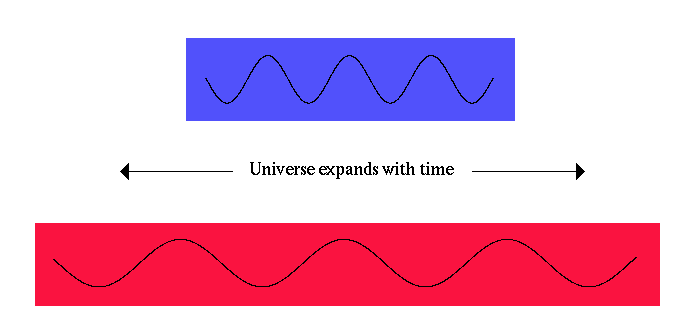
.. The radius of the Universe is given by R, notice that R is a quantity only seen in 2D space, not measured directly by the inhabitants of the 1D circle unless they measure 2pR by walking around the Universe. Now, we let the Universe expand by a factor of 2, R becomes 2R. The distance between the galaxies becomes 2S, but the co-moving coordinate, angle q remains unchanged. Since the distance between the galaxies has increased, then the galaxies will appear to have moved apart by S/time of expansion. When, in fact, the galaxies have not moved at all, the space between them has increased. .. Expanding spacetime also explains the redshift of galaxies, which is interpreted as Doppler motion. Since space expands, any photons traveling through that space (from distant galaxies to us) must also expand, i.e. the photons are `stretched' as they travel across the Universe. |
|
.. So the redshift we see for distant galaxies is really an effect of spacetime expanding, not real motion. This is good because some of the redshifts for the most distant galaxies have recessional velocities in excess to the speed of light. But this is not a contradiction for special relativity since the space is expanding, not true motion. We will also see that photons created as gamma rays in the early Universe are now redshifted to the microwave region of the spectrum to make up what is called the cosmic microwave background (CMB). |
|
Can the Universe be finite in size? If so,
what is "outside" the Universe? The answer to both these questions
involves a discussion of the intrinsic geometry of the Universe.
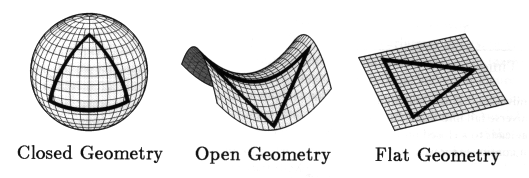
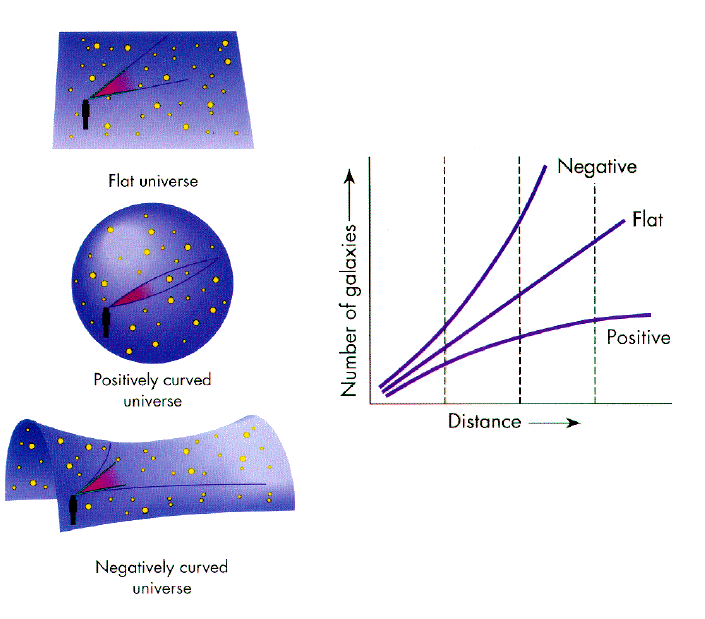
.. There are basically three possible shapes to the Universe; a flat Universe (Euclidean or zero curvature), a spherical Universe (positive curvature) or a hyperbolic Universe (negative curvature). Note that this curvature is similar to spacetime curvature due to stellar masses except that the entire mass of the Universe determines the curvature. So a high mass Universe can have positive curvature, a low mass Universe might have negative curvature. |
.. |
.. All three geometries are classes of what is called Riemannian geometry, based on three possible states for parallel lines .. .. or one can think of triangles where for a flat Universe the angles of a triangle sum to 180 degrees, in a closed Universe the sum must be greater than 180, in an open Universe the sum must be less than 180. |
.. |
.. Standard cosmological observations do not say anything about how those volumes fit together to give the universe its overall shape--its topology. The three plausible cosmic geometries are consistent with many different topologies. For example, relativity would describe both a torus (a doughnutlike shape) and a plane with the same equations, even though the torus is finite and the plane is infinite. Determining the topology requires some physical understanding beyond relativity. |

|
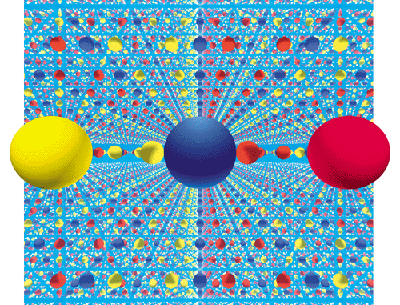
.. Like a hall of mirrors, the apparently endless universe might be deluding us. The cosmos could, in fact, be finite. The illusion of infinity would come about as light wrapped all the way around space, perhaps more than once--creating multiple images of each galaxy. A mirror box evokes a finite cosmos that looks endless. The box contains only three balls, yet the mirrors that line its walls produce an infinite number of images. Of course, in the real universe there is no boundary from which light can reflect. Instead a multiplicity of images could arise as light rays wrap around the universe over and over again. From the pattern of repeated images, one could deduce the universe's true size and shape. |
.. |
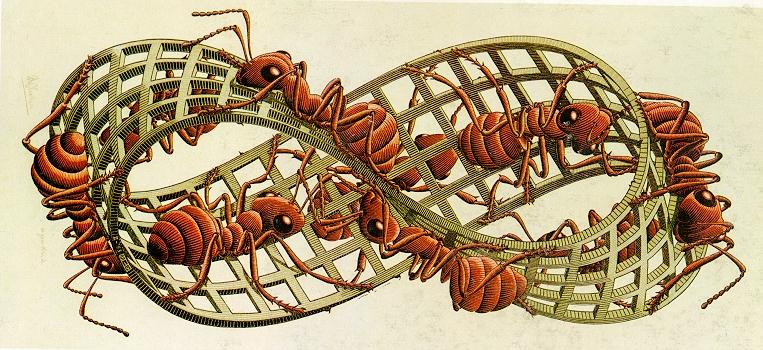
.. Topology shows that a flat piece of spacetime can be folded into a torus when the edges touch. In a similar manner, a flat strip of paper can be twisted to form a Moebius Strip. |
.. |
.. The 3D version of a moebius strip is a Klein Bottle, where spacetime is distorted so there is no inside or outside, only one surface. |

.. |
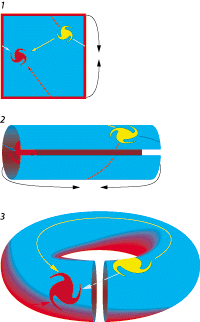
.. The usual assumption is that the universe is, like a plane, "simply connected," which means there is only one direct path for light to travel from a source to an observer. A simply connected Euclidean or hyperbolic universe would indeed be infinite. But the universe might instead be "multiply connected," like a torus, in which case there are many different such paths. An observer would see multiple images of each galaxy and could easily misinterpret them as distinct galaxies in an endless space, much as a visitor to a mirrored room has the illusion of seeing a huge crowd. |
.. |
.. One possible finite geometry is donutspace or more properly known as the Euclidean 2-torus, is a flat square whose opposite sides are connected. Anything crossing one edge reenters from the opposite edge (like a video game see 1 above). Although this surface cannot exist within our three-dimensional space, a distorted version can be built by taping together top and bottom (see 2 above) and scrunching the resulting cylinder into a ring (see 3 above). For observers in the pictured red galaxy, space seems infinite because their line of sight never ends (below). Light from the yellow galaxy can reach them along several different paths, so they see more than one image of it. A Euclidean 3-torus is built from a cube rather than a square. |

.. |
.. A finite hyperbolic space is formed by an octagon whose opposite sides are connected, so that anything crossing one edge reenters from the opposite edge (top left). Topologically, the octagonal space is equivalent to a two-holed pretzel (top right). Observers who lived on the surface would see an infinite octagonal grid of galaxies. Such a grid can be drawn only on a hyperbolic manifold--a strange floppy surface where every point has the geometry of a saddle (bottom). |
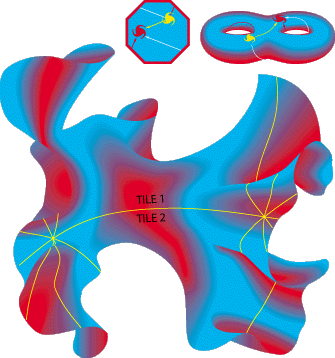
.. |
.. Its important to remember that the above images are 2D shadows of 4D space, it is impossible to draw the geometry of the Universe on a piece of paper, it can only be described by mathematics. All possible Universes are finite since there is only a finite age and, therefore, a limiting horizon. The geometry may be flat or open, and therefore infinite in possible size (it continues to grow forever), but the amount of mass and time in our Universe is finite. |
|
Measuring the curvature of the Universe is
doable because of ability to see great distances with our new technology.
On the Earth, it is difficult to see that we live on a sphere. One stands
on a tall mountain, but the world still looks flat. One can see a ship
come over the horizon, but that was thought to be atmospheric refraction
for a long time.
.. Our current technology allows us to see over 80% of the size of the Universe, sufficient to measure curvature. Any method to measure distance and curvature requires a standard `yardstick', some physical characteristic that is identifiable at great distances and does not change with lookback time. |
.. |
.. The three primary methods to measure curvature are luminosity, scale length and number. Luminosity requires an observer to find some standard `candle', such as the brightest quasars, and follow them out to high redshifts. Scale length requires that some standard size be used, such as the size of the largest galaxies. Lastly, number counts are used where one counts the number of galaxies in a box as a function of distance. .. To date all these methods have been inconclusive because the brightest, size and number of galaxies changes with time in a ways that we have not figured out. So far, the measurements are consistent with a flat Universe, which is popular for aesthetic reasons. |