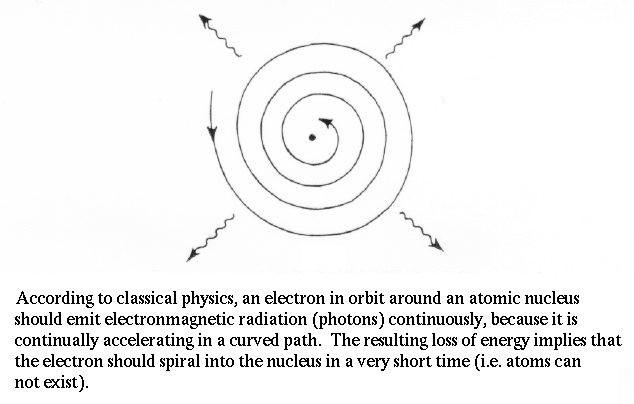
|
The UV catastrophe and the dilemma of spectral lines were already serious problems for attempts to understand how light and matter interact. Planck also noticed another fatal flaw in our physics by demonstrating that the electron in orbit around the nucleus accelerates. Acceleration means a changing electric field (the electron has charge), when means photons should be emitted. But, then the electron would lose energy and fall into the nucleus. Therefore, atoms shouldn't exist! |

.. |
.. To resolve this problem, Planck made a wild assumption that energy, at the sub-atomic level, can only be transfered in small units, called quanta. Due to his insight, we call this unit Planck's constant (h). The word quantum derives from quantity and refers to a small packet of action or process, the smallest unit of either that can be associated with a single event in the microscopic world. .. Quantum, in physics, discrete natural unit, or packet, of energy, charge, angular momentum, or other physical property. Light, for example, appearing in some respects as a continuous electromagnetic wave, on the submicroscopic level is emitted and absorbed in discrete amounts, or quanta; and for light of a given wavelength, the magnitude of all the quanta emitted or absorbed is the same in both energy and momentum. These particle-like packets of light are called photons, a term also applicable to quanta of other forms of electromagnetic energy such as X rays and gamma rays. .. All phenomena in submicroscopic systems (the realm of quantum mechanics) exhibit quantization: observable quantities are restricted to a natural set of discrete values. When the values are multiples of a constant least amount, that amount is referred to as a quantum of the observable. Thus Planck's constant h is the quantum of action, and h/ (i.e., h/2 ) is the quantum of angular momentum, or spin. |
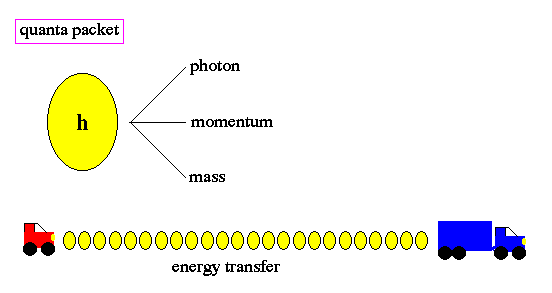
.. |
.. Changes of energy, such as the transition of an electron from one orbit to another around the nucleus of an atom, is done in discrete quanta. Quanta are not divisible. The term quantum leap refers to the abrupt movement from one discrete energy level to another, with no smooth transition. There is no "inbetween" . .. The quantization, or "jumpiness" of action as depicted in quantum physics differs sharply from classical physics which represented motion as smooth, continuous change. Quantization limits the energy to be transfered to photons and resolves the UV catastrophe problem. |
|
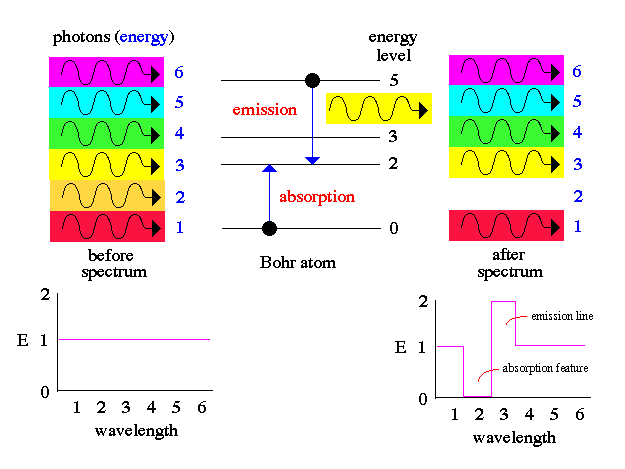
The results from spectroscopy (emission and
absorption spectra) can only be explained if light has a particle nature
as shown by Bohr's atom and the photon description of light.
.. This dualism to the nature of light is best demonstrated by the photoelectric effect, where a weak UV light produces a current flow (releases electrons) but a strong red light does not release electrons no matter how intense the red light. .. An unusual phenomenon was discovered in the early 1900's. If a beam of light is pointed at the negative end of a pair of charged plates, a current flow is measured. A current is simply a flow of electrons in a metal, such as a wire. Thus, the beam of light must be liberating electrons from one metal plate, which are attracted to the other plate by electrostatic forces. This results in a current flow. .. In classical physics, one would expect the current flow to be proportional to the strength of the beam of light (more light = more electrons liberated = more current). However, the observed phenomenon was that the current flow was basically constant with light strength, yet varied strong with the wavelength of light such that there was a sharp cutoff and no current flow for long wavelengths. .. Einstein successful explained the photoelectric effect within the context of the new physics of the time, quantum physics. In his scientific paper, he showed that light was made of packets of energy quantum called photons. Each photon carries a specific energy related to its wavelength, such that photons of short wavelength (blue light) carry more energy than long wavelength (red light) photons. To release an electron from a metal plate required a minimal energy which could only be transfered by a photon of energy equal or greater than that minimal threshold energy (i.e. the wavelength of the light had to be a sufficiently short). Each photon of blue light released an electron. But all red photons were too weak. The result is no matter how much red light was shown on the metal plate, there was no current. .. The photoelectric earned Einstein the Nobel Prize, and introduced the term "photon" of light into our terminology. |
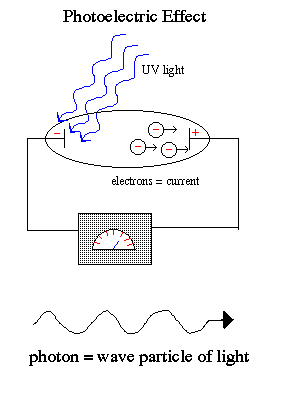
.. |
.. Einstein explained that light exists in a particle-like state as packets of energy (quanta) called photons. The photoelectric effect occurs because the packets of energy carried by each individual red photons are too weak to knock the electrons off the atoms no matter how many red photons you beamed onto the cathode. But the individual UV photons were each strong enough to release the electron and cause a current flow. .. It is one of the strange, but fundamental, concepts in modern physics that light has both a wave and particle state (but not at the same time), called wave-particle dualism. .. Wave/particle duality is the possession by physical entities (such as light and electrons) of both wavelike and particle-like characteristics. On the basis of experimental evidence, the German physicist Albert Einstein first showed (1905) that light, which had been considered a form of electromagnetic waves, must also be thought of as particle-like, or localized in packets of discrete energy. The French physicist Louis de Broglie proposed (1924) that electrons and other discrete bits of matter, which until then had been conceived only as material particles, also have wave properties such as wavelength and frequency. Later (1927) the wave nature of electrons was experimentally established. An understanding of the complementary relation between the wave aspects and the particle aspects of the same phenomenon was announced in 1928. .. Dualism is not such a strange concept, consider the following picture, are the swirls moving or not or both? |

|
Perhaps the foremost scientists of the 20th
century was Niels Bohr, the first to apply Planck's quantum idea to
problems in atomic physics. In the early 1900's, Bohr proposed a quantum
mechanical description of the atom to replace the early model of
Rutherford.
.. In 1913 Bohr proposed his quantized shell model of the atom to explain how electrons can have stable orbits around the nucleus. The motion of the electrons in the Rutherford model was unstable because, according to classical mechanics and electromagnetic theory, any charged particle moving on a curved path emits electromagnetic radiation; thus, the electrons would lose energy and spiral into the nucleus. To remedy the stability problem, Bohr modified the Rutherford model by requiring that the electrons move in orbits of fixed size and energy. The energy of an electron depends on the size of the orbit and is lower for smaller orbits. Radiation can occur only when the electron jumps from one orbit to another. The atom will be completely stable in the state with the smallest orbit, since there is no orbit of lower energy into which the electron can jump. .. Bohr's starting point was to realize that classical mechanics by itself could never explain the atom's stability. A stable atom has a certain size so that any equation describing it must contain some fundamental constant or combination of constants with a dimension of length. The classical fundamental constants--namely, the charges and the masses of the electron and the nucleus--cannot be combined to make a length. Bohr noticed, however, that the quantum constant formulated by the German physicist Max Planck has dimensions which, when combined with the mass and charge of the electron, produce a measure of length. Numerically, the measure is close to the known size of atoms. This encouraged Bohr to use Planck's constant in searching for a theory of the atom. |
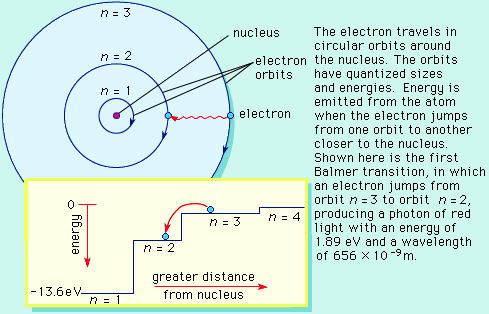
.. |
.. Planck had introduced his constant in 1900 in a formula explaining the light radiation emitted from heated bodies. According to classical theory, comparable amounts of light energy should be produced at all frequencies. This is not only contrary to observation but also implies the absurd result that the total energy radiated by a heated body should be infinite. Planck postulated that energy can only be emitted or absorbed in discrete amounts, which he called quanta (the Latin word for "how much"). The energy quantum is related to the frequency of the light by a new fundamental constant, h. When a body is heated, its radiant energy in a particular frequency range is, according to classical theory, proportional to the temperature of the body. With Planck's hypothesis, however, the radiation can occur only in quantum amounts of energy. If the radiant energy is less than the quantum of energy, the amount of light in that frequency range will be reduced. Planck's formula correctly describes radiation from heated bodies. Planck's constant has the dimensions of action, which may be expressed as units of energy multiplied by time, units of momentum multiplied by length, or units of angular momentum. For example, Planck's constant can be written as h = 6.6x10-34 joule seconds. .. Using Planck's constant, Bohr obtained an accurate formula for the energy levels of the hydrogen atom. He postulated that the angular momentum of the electron is quantized--i.e., it can have only discrete values. He assumed that otherwise electrons obey the laws of classical mechanics by traveling around the nucleus in circular orbits. Because of the quantization, the electron orbits have fixed sizes and energies. The orbits are labeled by an integer, the quantum number n. .. With his model, Bohr explained how electrons could jump from one orbit to another only by emitting or absorbing energy in fixed quanta. For example, if an electron jumps one orbit closer to the nucleus, it must emit energy equal to the difference of the energies of the two orbits. Conversely, when the electron jumps to a larger orbit, it must absorb a quantum of light equal in energy to the difference in orbits. The Bohr model basically assigned discrete orbits for the electron, multiples of Planck's constant, rather than allowing a continuum of energies as allowed by classical physics. .. The power in the Bohr model was its ability to predict the spectra of light emitted by atoms. In particular, its ability to explain the spectral lines of atoms as the absorption and emission of photons by the electrons in quantized orbits. |
.. |
.. Our current understanding of atomic structure was formalized by Heisenberg and Schroedinger in the mid-1920's where the discreteness of the allowed energy states emerges from more general aspects, rather than imposed as in Bohr's model. The Heisenberg/Schroedinger quantum mechanics have consistent fundamental principles, such as the wave character of matter and the incorporation of the uncertainty principle. .. In principle, all of atomic and molecular physics, including the structure of atoms and their dynamics, the periodic table of elements and their chemical behavior, as well as the spectroscopic, electrical, and other physical properties of atoms and molecules, can be accounted for by quantum mechanics => fundamental science. |
|
Perhaps one of the key questions when Bohr offered his quantized orbits as an explanation to the UV catastrophe and spectral lines is, why does an electron follow quantized orbits? The response to this question arrived from the Ph.D. thesis of Louis de Broglie in 1923. de Broglie argued that since light can display wave and particle properties, then perhaps matter can also be a particle and a wave too. |
.. |
..  |
.. |
.. 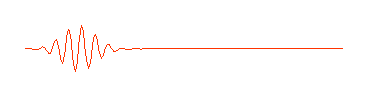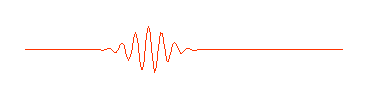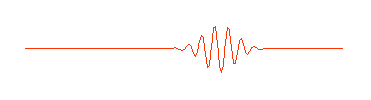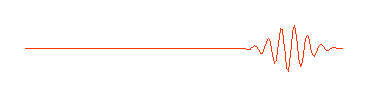 |
.. |
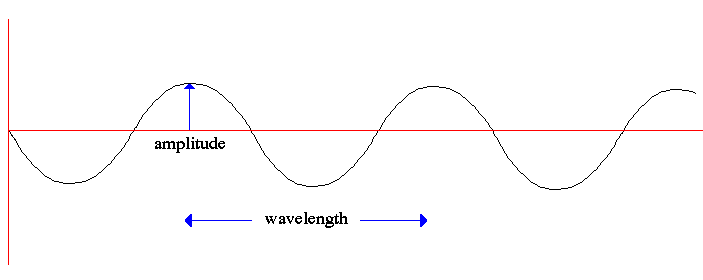
.. So a photon, or a free moving electron, can be thought of as a wave packet, having both wave-like properties and also the single position and size we associate with a particle. There are some slight problems, such as the wave packet doesn't really stop at a finite distance from its peak, it also goes on for every and every. Does this mean an electron exists at all places in its trajectory? .. de Broglie also produced a simple formula that the wavelength of a matter particle is related to the momentum of the particle. So energy is also connected to the wave property of matter. |
.. |
.. 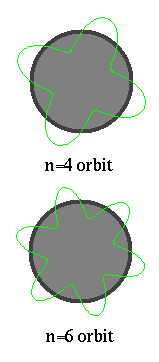 .. The electron matter wave is both finite and unbounded (remember the 1st lecture on math). But only certain wavelengths will `fit' into an orbit. If the wavelength is longer or shorter, then the ends do not connect. Thus, de Broglie explains the Bohr atom in that on certain orbits can exist to match the natural wavelength of the electron. If an electron is in some sense a wave, then in order to fit into an orbit around a nucleus, the size of the orbit must correspond to a whole number of wavelengths. |
.. |
.. Notice also that this means the electron does not exist at one single spot in its orbit, it has a wave nature and exists at all places in the allowed orbit. Thus, a physicist speaks of allowed orbits and allowed transitions to produce particular photons (that make up the fingerprint pattern of spectral lines). And the Bohr atom really looks like the following diagram: |
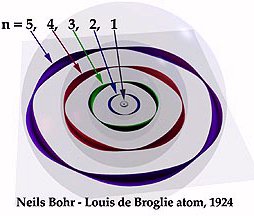
.. |
.. While de Broglie waves were difficult to accept after centuries of thinking of particles are solid things with definite size and positions, electron waves were confirmed in the laboratory by running electron beams through slits and demonstrating that interference patterns formed. .. How does the de Broglie idea fit into the macroscopic world? The length of the wave diminishes in proportion to the momentum of the object. So the greater the mass of the object involved, the shorter the waves. The wavelength of a person, for example, is only one millionth of a centimeter, much to short to be measured. This is why people don't `tunnel' through chairs when they sit down. |
.. |
.. The idea that an electron is a wave around the atom, instead of a particle in orbit begs the question of `where' the electron is at any particular moment. The answer, by experimentation, is that the electron can be anywhere around the atom. But 'where' is not evenly distributed. The electron as a wave has a maximum chance of being observed where the wave has the highest amplitude. Thus, the electron has the highest probability to exist at a certain orbit. .. Where probability is often used in physics to describe the behavior of many objects, this is the first instance of an individual object, an electron, being assigned a probability for a Newtonian characteristic such as position. Thus, an accurate description of an electron orbit is one where we have a probability field that surrounds the nucleus, as shown below: |
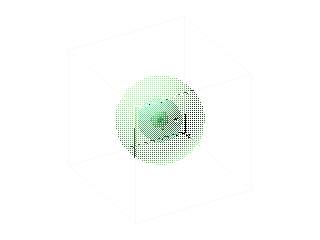
.. |
.. For more complicated orbits, and higher electron shells, the probability field becomes distorted by other electrons and their fields, like the following example: |

.. |
.. Thus, for the first time, the concept of existence begins to take on an elusive character at the subatomic level. |